How To Find Big Oh Of Floor Function

Some say int 3 65 4 the same as the floor function others say int 3 65 3 the neighbouring integer closest to zero or just throw away the 65.

How to find big oh of floor function.

The first post explains big o from a self taught programmer s perspective the third article talks about understanding the formal definition of big o. So at infinity one has frac x 4 9x 3 4x 7 x 4 1 frac 9 x frac 4 x 2 frac 7 x 4 by taking x sufficiently large one can make frac f x g x leq 2 and we are done. If you have f n 3n 3 20n 2 5 and you want to see if it s o g n where g n n 3 i believe you can take the limit of f n g n as n infinity. In brief in this article we discuss analysis of algorithm using big o asymptotic notation in complete details.

For this function that term is 4x 3. Because the limit is 3 you can see that 3n 3 20n 2 5 only grows as fast as n 3. Recurrence relations it s not easy trying to determine the asymptotic complexity using big oh of recursive functions without an easy to use but underutilized tool. K 1 which is the definition of floor function and conclude they are equal.

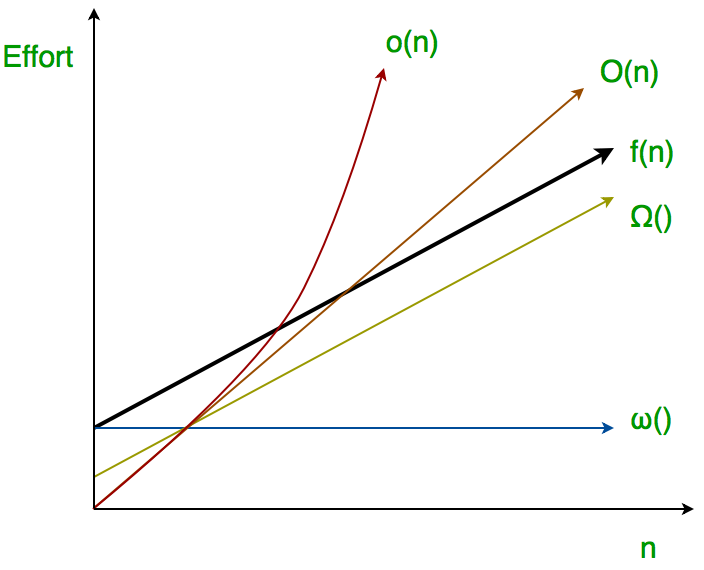
Then put a big o in front. Using the definitions of big oh and ω find the upper and lower bounds for the following expressions. Let math f n 2n 3 30n 2 math now at the surface you may be inclined to say well that 30 seems to be bigger than the 2 but remember we are interested in the asymptotics of these things so these constants in these circumstances do not matter. Proof involving big o and floor.

Big o analysis of algorithms. Ask question asked 4 years 8 months ago. The int function short for integer is like the floor function but some calculators and computer programs show different results when given negative numbers. Now just get rid of the constant out front to get x 3.

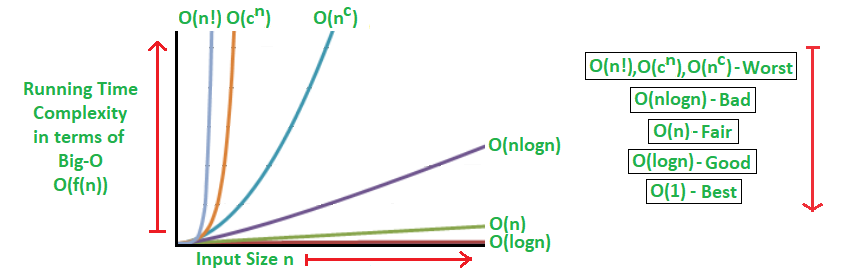
If the function is not too unweildy it s pretty easy to do. In our previous articles on analysis of algorithms we had discussed asymptotic notations their worst and best case performance etc. Find big oh for nested for loop with floor function. This web page gives an introduction to how recurrence relations can be used to help determine the big oh running time of recursive functions.

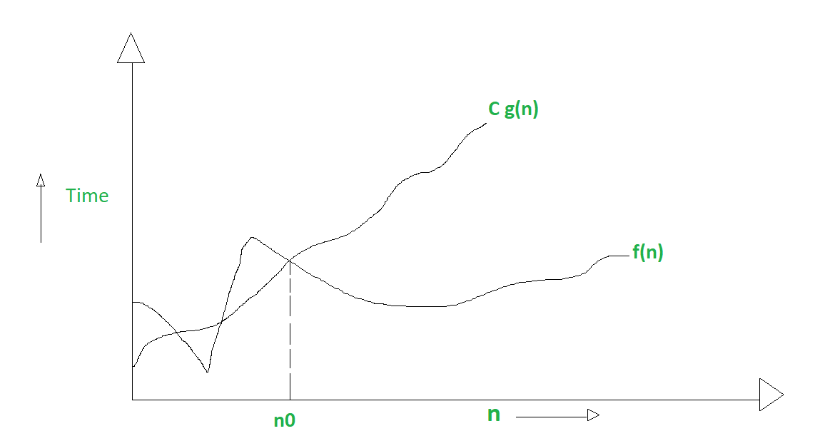
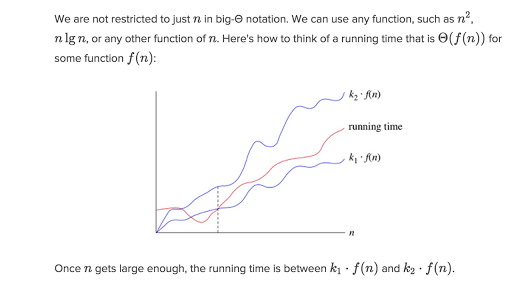
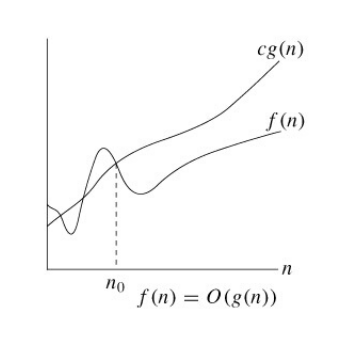
Let me give a basic example for determining the asymptotic bound in terms of big oh. The big o notation defines an upper bound of an algorithm it bounds a function only from above. Lokk for the highest order term the term that grows faster than the other terms as x gets larger. C 1 3 n c 2 n 4 where the constants are positive integers.

Big oh for recursive functions. The definition of big o says that f o g in the neighborhood of x 0 if and only if frac f g is bounded in that neighborhood. So now that we know what big o is how do we calculate the big o classification of a given function it s just as easy as following along with your code and counting along the way. Consider the function f x 4x 3 7x 2 log x 3x 8.